| |

|
|
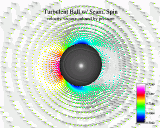
The spinning tennis ball lies around the border of being both predominantly laminar and predominately
turbulent. When we look at the picture, we see that the vectors at the front of the ball are directed
smoothly along the surface of the ball. Behind the ball, the vectors start to leave the surface and become
jumbled. This type of separation tends to affect the flight of the ball. This is why balls that are meant
to be able to curve often have seams, that break up the flow further and help create turbulence. However,
the predominate reason why the ball curves, is because of its spinning surface. The no-slip condition
requires that there is no relative motion allowed between the air and the contact point of the ball (we
can see in the vector field that the vectors shrink to nothing as we get closer to the surface). Therefore
the ball will tend to drag the air around faster in the direction it's spinning and create a pressure
difference, causing the ball to curve. The end result is the same as an airplane wing as the ball "lifts"
in the direction the air is moving faster.
Contributed by Eric Beights, Princeton University.
|
|