11. Drag of Blunt and Streamlined Bodies

We can see the role played by friction drag (sometimes called viscous drag) and pressure drag (sometimes called form drag or profile drag) by considering an airfoil at different angles of attack. At small angles of attack, the boundary layers on the top and bottom surface experience only mild pressure gradients, and they remain attached along almost the entire chord length. The wake is very small, and the drag is dominated by the viscous friction inside the boundary layers. However, as the angle of attack increases, the pressure gradients on the airfoil increase in magnitude. In particular, the adverse pressure gradient on the top rear portion of the airfoil may become sufficiently strong to produce a separated flow. This separation will increase the size of the wake, and the pressure losses in the wake due to eddy formation Therefore the pressure drag increases. At a higher angle of attack, a large fraction of the flow over the top surface of the airfoil may be separated, and the airfoil is said to be stalled. At this stage, the pressure drag is much greater than the viscous drag .

When the drag is dominated by viscous drag, we say the body is streamlined, and when it is dominated by pressure drag, we say the body is bluff. Whether the flow is viscous-drag dominated or pressure-drag dominated depends entirely on the shape of the body. A streamlined body looks like a fish, or an airfoil at small angles of attack, whereas a bluff body looks like a brick, a cylinder, or an airfoil at large angles of attack. For streamlined bodies, frictional drag is the dominant source of air resistance. For a bluff body, the dominant source of drag is pressure drag. For a given frontal area and velocity, a streamlined body will always have a lower resistance than a bluff body. For example, the drag of a cylinder of diameter D can be ten times larger than a streamlined shape with the same thickness (see figure 11.1).

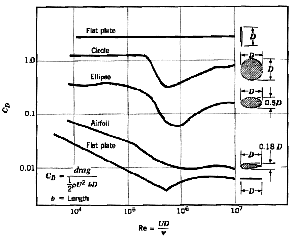Figure 11.1 Drag coefficients of blunt and streamlined bodies. From Munson, Young and Okiishi, Fundamentals of Fluid Mechanics, John Wiley & Sons, 1998.

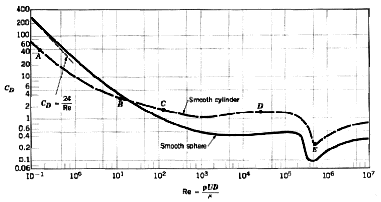
Cylinders and spheres are considered bluff bodies because at large Reynolds numbers the drag is dominated by the pressure losses in the wake. The variation of the drag coefficient with Reynolds number is shown in figure 11.2, and the corresponding flow patterns are shown in figure 11.3. We see that as the Reynolds number increases the variation in the drag coefficient (based on cross-sectional area) decreases, and over a large range in Reynolds number it is nearly constant.

Figure 11.2 Drag coefficient as a function of Reynolds number for smooth circular cylinders and smooth spheres. From Munson, Young and Okiishi, Fundamentals of Fluid Mechanics, John Wiley & Sons, 1998.

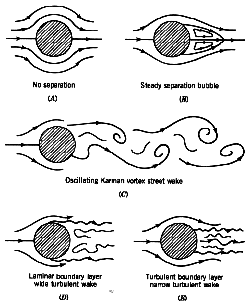Figure 11.3 Flow patterns for flow over a cylinder: (A) Reynolds number = 0.2; (B) 12; (C) 120; (D) 30,000; (E) 500,000. Patterns correspond to the points marked on figure 11.2. From Munson, Young and Okiishi, Fundamentals of Fluid Mechanics, John Wiley & Sons, 1998.

At a Reynolds number between 10^5 and 10^6, the drag coefficient takes a sudden dip. The size of the wake decreases, indicating that the boundary layer separation on the cylinder or sphere occurs further along the surface than before. What has happened? The phenomenon is related to the differences between laminar and turbulent boundary layer. The boundary layer and its interaction with the local pressure gradient plays a major role in affecting the flow over a cylinder. In particular, near the shoulder, the pressure gradient changes from being negative (decreasing pressure) to positive (increasing pressure). The force due to pressure differences changes sign from being an accelerating force to being a retarding force. In response, the flow slows down. However, the fluid in the boundary layer has already given up some momentum because of viscous losses and viscous friction, and it does not have enough momentum to overcome the retarding force. Some fluid near the wall actually reverses direction, and the flow separates.

A laminar boundary layer has less momentum near the wall than a turbulent boundary layer, as shown in figure 11.4, because turbulence is a very effective mixing process. More importantly, turbulent transport of momentum is very effective at replenishing the near-wall momentum. So when a turbulent boundary layer enters a region of adverse pressure gradient, it can persist for a longer distance without separating (compared to a laminar flow) because the momentum near the wall is higher to begin with, and it is continually (and quickly) being replenished by turbulent mixing .

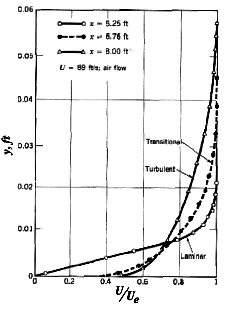Figure 11.4 Boundary layer profiles for laminar and turbulent flow. From Schlichting, Boundary Layer Theory, 7th ed., McGraw-Hill, 1979.

The boundary layer over the front face of a sphere or cylinder is laminar at lower Reynolds numbers, and turbulent at higher Reynolds numbers. When it is laminar (Re < 10^5), separation starts almost as soon as the pressure gradient becomes adverse (very near the shoulder, figure 11.3D), and a large wake forms. When it is turbulent (Re > 10^6), separation is delayed (to a point about 20^o past the shoulder, figure 11.3E) and the wake is correspondingly smaller.

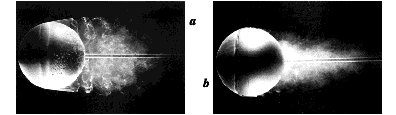
It follows that, if the boundary layer of a sphere can be made turbulent at a lower Reynolds number, then the drag should also go down at that Reynolds number. This is the case, as we can show by using a trip wire. A trip wire is simply a wire located on the front face of the sphere and it introduces a large disturbance into the boundary layer. This disturbance causes an early transition to turbulence, and it effect on the size of the wake, and the total drag is quite dramatic, as shown in figure 11.5.

Figure 11.5 Flow over a sphere: (a) Reynolds number = 15,000; (b) Reynolds number = 30,000, with trip wire. From Werlé, ONERA, 1980.