|
|
 |
8. Flows With Friction
If there are no shear stresses present, there is no fluid deformation, and the behavior of a
fluid is described by the bulk modulus relating the pressure and the compression strain. In
the presence of a shear stress, however, the shear angle will grow indefinitely if the shear
stress is maintained. The shear stress is not related to the magnitude of the shear angle,
as in solids, but to the rate at which the angle is changing. For many fluids, the
relationship is linear, so that
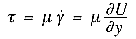
where the coefficient of proportionality is called the dynamic viscosity of
the fluid, or simply the fluid viscosity, and it is a material property of the fluid.
Fluids which obey this
linear relationship between stress and strain rate are called Newtonian fluids. Most
common fluids are Newtonian, including air and water over very wide ranges of pressures and
temperatures.
However, not all fluids obey a Newtonian stress-strain relationship. An enormous variety
of ``visco-elastic'' fluids exist that obey more complicated constitutive relationships,
such as nonlinear relationships, similar to plastic deformation of solids, or history
effects, where the stress history needs to be known before the deformation can be
predicted. Such fluids are commonly encountered in the plastics and
chemical industries.
Flows inside ducts, channels and pipes are very important because they occur in many
practical applications (water pipes, air conditioning ducts, gas lines, ventilation
shafts, heat exchanger tubes, etc.). Friction is usually important in
these flows because there is a resistance to relative motion: when one layer of fluid is
moving with respect to an adjacent layer, there exists friction between the layers. The
amount of friction depends on the fluid viscosity and the velocity gradient (that
is, the relative velocity between fluid layers). The velocity gradients are
set up by the no-slip condition at the wall. When a fluid is in contact
with a solid surface, there can be no
relative motion between the fluid in contact with the solid surface and the surface itself:
if the wall has zero velocity, then the fluid in contact with the wall has zero velocity
also.
To see how the no-slip condition arises, and how the no-slip condition and the fluid
viscosity lead to frictional stresses, we can examine the conditions at a solid surface on
a molecular scale. When a fluid is stationary, its molecules are in a constant state of
motion with a random velocity
v. For a gas, v is equal to the
speed of sound. When a fluid is in motion, there is superimposed on this random
velocity a mean velocity V, sometimes called the bulk velocity, which is the velocity at
which
fluid from one place to another.
At the interface between the fluid and the surface, there exists an
attraction between the molecules or atoms that make up the fluid and those that make up the
solid. This attractive force is strong enough
to reduce the bulk velocity of the fluid to zero. So the
bulk velocity of the fluid must change from whatever its value is far away from the wall to
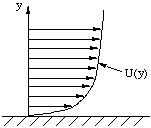
a value of zero at the wall (figure 8.1). This is called the no-slip condition.
 |
 |
Figure 8.1 Velocity profile in a boundary layer.
|
The most powerful consequence of the no-slip condition is the appearance of strong
velocity gradients near the wall. This region is often very thin, and it is then called a
boundary layer (see figures 8.2 and 8.3). Within the
boundary layer, adjacent layers of fluid are in relative motion, and because all fluids have
viscosity, there will be friction between the layers as they slide over each other. In
other words, viscous stresses are produced, with a magnitude given by the viscosity times
the velocity gradient. These viscous, frictional stresses cause energy dissipation in the
fluid, which appears as heat. Since it takes an enormous amount of energy to heat a gas or
liquid to an appreciable temperature, this heat generation is not usually important at
subsonic speeds. At supersonic speeds, however, sufficient heat is generated by viscous
dissipation in the boundary layer to change the density of the fluid significantly.
 |
 |
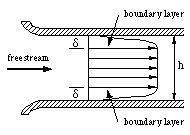
Figure 8.2 Flow in a channel, showing boundary layers near the walls.
|
 |
 |
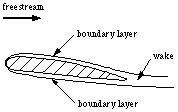
Figure 8.3
Flow over an airfoil, showing boundary layers near the surface, and the formation of a
wake.
|
Inside a pipe or a channel, the boundary layers grow in thickness as more and more of the fluid is
affected by viscous friction originating from the gradients set up by the no-slip condition.
The layers meet in the middle and merge, and the flow reaches an asymptotic state
called fully-developed flow (figure 8). Boundary layers in an external flow, such as the airfoil shown in figure 8.3,
the boundary layers continue to grow along the length of
the body. At the trailing edge, the boundary layers from the two sides meet and form the wake.
Since friction is always present when there is relative motion between fluid
layers, and because boundary layers are always formed near solid surfaces, a certain
amount of energy is continually given up as heat when a body moves through a fluid. The force acting on a body due to the viscous resistance of the
surrounding fluid is called the drag force and it acts in the direction opposite to the
direction of motion. As a consequence of the fluid friction, the entropy always rises, and the flow is not reversible.
|
 |